Subtraction | Definition, Meaning, and Types

Mental math is the main foundation behind every logical process. It is based on a few fundamental operators. One of these operators is subtraction. It is the core building block of mathematics. But why is it important? Here is the main reason: it helps in understanding the concept of “How much less” or “what’s left.” It solves real-world problems like calculating time left for an event, reducing fractions, or debugging binary code. 

It also strengthens your mental math skills by encouraging logical thinking and number sense. This mathematical operator provides a base for other complex concepts like fraction subtraction, binary subtraction, and even time subtraction. In this guide, we’ll learn how subtraction works mentally and practically by exploring multiple tools to master this core math operation in everyday life

Subtraction

Subtraction is one of the core arithmetic operators, which is widely used in solving real-life problems. Let’s begin with its definition, which is stated as

“It is the mathematical process of finding the difference between two numbers, values, or quantities.”

Meaning

In simple terms, subtraction in math tells us how much less one number is compared to another. This mathematical operator is binary, as it works with two operands. It is the opposite of addition. It is more than what we think—just taking away. It gives the answers to conceptual questions like what remains, what’s missing, or what needs to be removed to reach a certain value. 

Symbol

The symbol, denoted by “− ”, is also known as the minus sign. It is a fundamental mathematical symbol used to represent the operation of subtraction. It tells us to take away one value from another or to find the difference between two numbers. In math, when you see the minus sign between two numbers, such as 10 − 4,  it means you are subtracting 4 from 10.

The minus sign in math serves two important purposes:

1. It indicates the operation of subtracting numbers, as in 9 − 5 = 4.
2. It is also used to represent negative integers, such as −7 or −15, which show values less than zero.
   

The basic concept of the minus sign is not just about “taking away.” It plays a key role in expressing the values below zero, which are negative numbers. Understanding how to read and use the minus sign correctly is essential for solving both basic and advanced problems.

Whether you’re solving a subtraction sentence, identifying negative values, or working with real-life math problems, the symbol “−” is the starting point that tells you the operation and the direction of change.

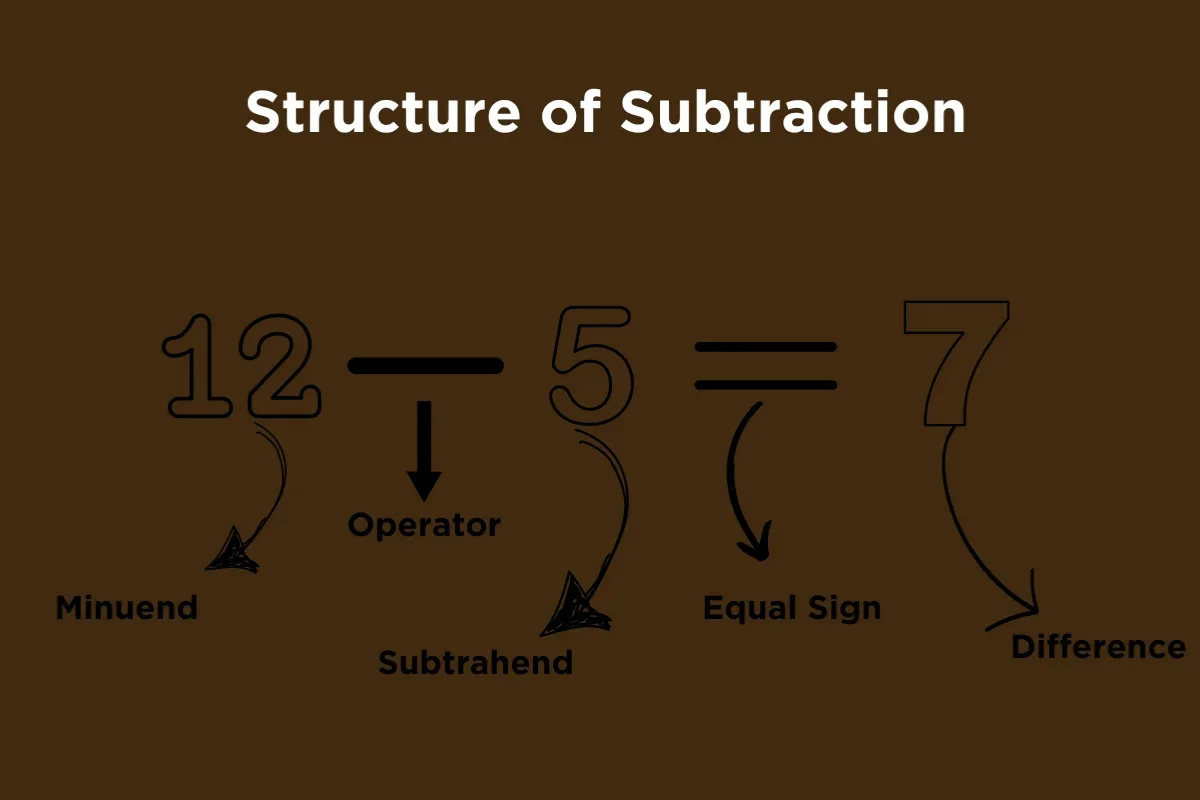
Parts

Before solving real-life examples, it is essential to understand the parts involved to perform subtraction correctly. You can understand the subtraction formula and the parts of a subtraction sentence from the following mathematical structure. The basic formula is as

Minuend − Subtrahend = Difference

This formula tells us exactly what is being subtracted and what the result will be. Let’s break down the parts to learn further concepts of it. 

Minuend

The first number in an expression—the number from which another number is subtracted.

Example

 In the example “15 − 7,” the number 15 is the minuend.

Subtrahend

The second number—the number that is being subtracted.

Example

The same example, which was “15 − 7,” the number 7 is the subtrahend.

Difference

Difference is the final result or the answer you get after performing the calculation.

Example

After solving this example, “15 − 7,” you will get the answer, which is equal to 8. This is called the difference.

This mathematical structure helps you to organize and solve real-life problems clearly, whether you are dealing with simple numbers, fractions, or even real-life word problems. Knowing how to identify the minuend, subtrahend, and difference also builds a strong foundation for mastering mental subtraction and more advanced mathematical topics.

Real-Life Word Problem 

After having deep knowledge it, let’s start to discuss the real-life example. As a matter of fact, it is not just a classroom concept; it is a daily-use mathematical operator. From shopping to tracking time, you often need to subtract to make quick and smart decisions. Let’s look at a real-life subtraction word problem that shows how subtracting numbers helps solve everyday situations:

Example

This is a real-life example, so make a scenario. Suppose John has 5 pencils. He gave 3 pencils to his classmates. How many pencils does he have left? To solve this real-life problem, we apply the basic formula:

Minuend − Subtrahend = Difference

Let’s break this problem into parts and understand how the formula works in the example:

Word Problem

John had 5 pencils. He gave 3 pencils to his classmates. How many pencils does he have left?Now we break this problem into parts of the sentence:

Minuend

This is the starting amount, which is the number of pencils John originally had. According to the above problem, the amount of pencils 5 is the minuend.

Subtrahend

This is the number that is being taken away—the pencils John gave away to his classmates. It was 3 pencils, so 3 is the subtrahend.

Difference

This is the result of subtracting 3 from 5, the number of pencils John has left after giving some away. The final result is 2, which is the difference.

Minuend (5) − Subtrahend (3) = Difference (2)

5 − 3 = 2

This simple and short real-life example shows how subtraction helps us calculate what’s left. This technique is a key skill in both educational and daily life. These skills are helpful for you, whether you’re managing money, measuring distances, or solving time-based questions. These techniques play a vital role in helping us make sense of numbers.

Types

Now, you have a strong knowledge about how this operator helps in real life. The above paragraphs built a strong foundation in understanding that it is not only about solving mathematical problems, but it is helpful in solving real-life problems. In fact, since real-life problems vary from time to time, the question arises, do we have different types or specific methods to handle these real-world problems? The answer is Yes! So, let’s explore these types one by one and see how each method fits for different mathematical and everyday situations.  

• Simple Subtraction
• Subtraction with Regrouping
• Mental Subtraction.
• Subtraction on Number Line
• Subtraction of Fractions
• Subtraction of Decimals
• Time Subtraction
• Subtraction of Negative Numbers
• Binary Subtraction
• Algebraic Subtraction

Simple Subtraction

Let’s consider a situation where the minuend is greater than the subtrahend. In this case, you can easily perform the subtraction operation without borrowing or regrouping any digits. So, this type is called simple or without regrouping subtraction.

It is so simple and straightforward that even young learners or early-grade students can solve these types of problems without any external help. This method builds a strong foundation in basic arithmetic operations. especially when working with single-digit or double-digit numbers.

Example

8  − 3 = 5

15 − 6 = 9

Subtraction with Regrouping

The second situation occurs when a digit in the subtrahend is larger than the digit above it in the minuend. How to solve this? In this case, you need to borrow from the next place value, which is known as subtraction with regrouping. This method helps solve multi-digit problems where simple technique isn’t possible without adjusting the digits.

Mental Subtraction 

One of the best techniques to solve a problem is to solve it by brain. Mental subtraction boosts you to subtract numbers in your head without writing anything. This type improves your number sense, mental agility, speed, and confidence. 

Common strategies are rounding numbers, breaking apart numbers, and using compensation.  Mental subtraction is highly useful in real-life scenarios, quick estimates, and mental math competitions.

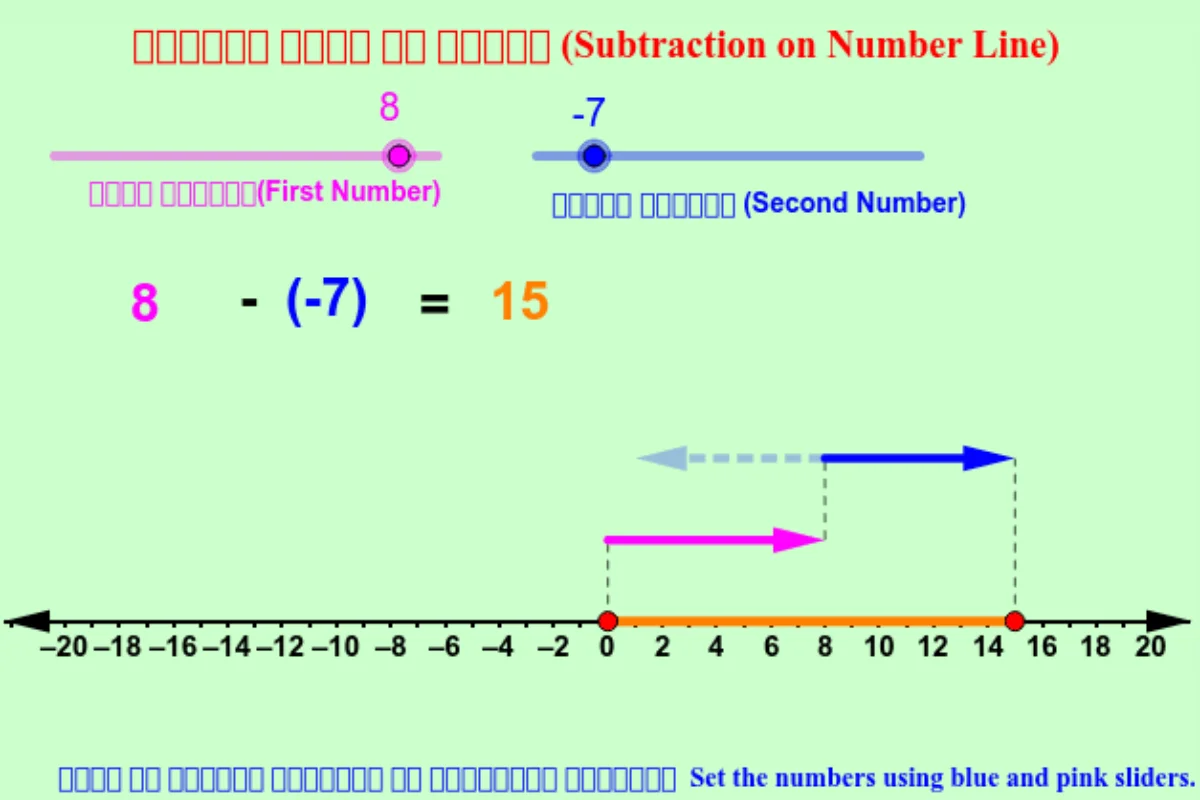
Number Line Subtraction

The best way to explain different basic concepts of mathematics is by visual methods. Number line subtraction is also a visual method where you can subtract numbers by counting backward on a straight line. You begin at the minuend and move to the left by the number of units equal to the subtrahend. 

This mental math technique helps you to better understand the concept and learn through visualization. The number line is especially effective for young learners of mathematics. 

Subtraction of Fractions

What happens if there is a fraction? You may get confused. But not more; here is the way to learn about fraction subtraction. 

Solving fractions in subtraction is a technique in which you are taking one fraction away from another. But you can’t directly subtract fractions unless both of the fractions have the same denominators. So, in this way there are two cases while solving fractions. 

To solve fractions by subtracting, first observe the denominators. If the denominators are already the same, you can directly subtract the numerators and write the answer with the common denominator. 

Subtraction of Decimals

Decimals, which are the essential part of the number system. What happens if these decimal numbers come in subtraction form? We face these problems on a daily basis. We often get stuck—but not anymore! Here is a short description for solving decimals. 

• The first step is to align the decimal points of both numbers vertically. 
• This step ensures that digits with the same place value line up, like tenths, hundredths, and so on. 
• If the numbers have a different number of digits after the decimal, you can add zeros to the end of the shorter number to make both numbers equal in length. 
• Once the decimal points and digits are aligned, subtract the numbers just like whole numbers, starting from the right side. 
• Finally, place the decimal point in the answer directly beneath the other decimal points. 

Time Subtraction

Time, which we deal with every single day. The question is, how to calculate time? How do we subtract hours, minutes, seconds, and even beyond? That’s where most of us get confused. And time subtraction feels tricky. But that ends here.

• First of all, write the given times in hours and minutes format. 
• Make sure the minutes of the starting time (minuend) are greater than or equal to the minutes of the time being subtracted (subtrahend). 
• If the minutes in the subtrahend are more, borrow 1 hour from the hours column and convert it into 60 minutes. 
• Then subtract the minutes first, followed by the hours. 
• Always subtract in the order of minutes first, then hours—just like you do with place values in numbers.

Subtraction of Negative Numbers

Numbers can be positive or negative. What if both or any one negative number appears in the subtraction problem? Usually, we feel irritated while solving problems of negative numbers. But that confusion ends here.

Before proceeding further, remember one key rule: subtracting a negative is the same as adding a positive.

In simple words, two negatives side by side turn into a plus. For example, 6 − (−3) becomes 6 + 3, which equals 9. 

Always watch for the signs: if you see a minus followed by a negative, convert it into a plus, and then solve normally. This rule helps clear the confusion whether you’re solving equations, balancing temperatures, or managing losses and gains.

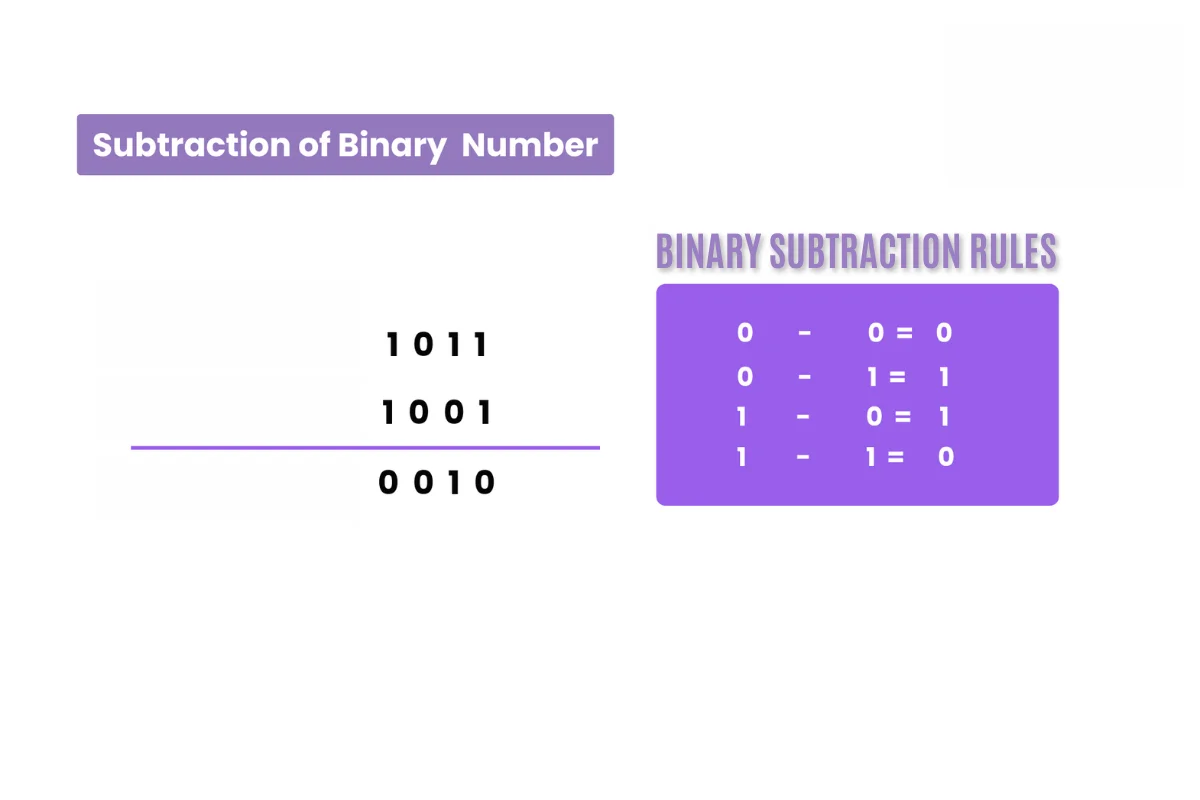
Binary Subtraction

Binary numbers—0 and 1—are the backbone of digital systems and computers. As the subtraction operator enters the binary world, many of us feel complicated and robotic. But here is a simplified explanation that makes it easy. 

Solving binary problems is just like solving decimal problems. 

• First of all, follow place values. 
• Learn the following four basic rules of binary numbers. 

1 − 0 = 1,
1 − 1 = 0,
0 − 0 = 0,
and most importantly, 0 − 1 = 1 with a borrow from the next higher bit. 

• If borrowing is needed, you borrow from the nearest 1 on the left, just like in decimal but with binary logic. 

Algebraic Subtraction

Algebra, which is the backbone of major concepts of mathematics, is a mix-up of numbers and alphabetic letters. This is another complicated situation to solve these problems. Most students get stuck when x, y, and constants all show up together. But that confusion ends here.

• For solving algebraic problem, carefully write both expressions with proper brackets. 
• In the very first step, remove the brackets while carefully changing the signs of the second expression. That’s because when you subtract, you’re actually adding the opposite. 
• After removing brackets, combine the like terms, meaning terms with the same variables and powers. Add or subtract their coefficients and write the simplified expression.

After covering the basic concepts, we will look to further advance concepts and problems in the next series of articles. 

Conclusion 

Subtraction is not about how to take away a number from another. It is a practical mathematical operator that is used in almost every real-world problem. It may seem like a basic math operation, but we’ve explored it from every aspect, like for academic learning and real-world problem-solving. 

Now, after going through this article, you learn about basic to advanced concepts. We start from the beginning—the definition and meaning—and conclude with every possible type. Each method builds a foundation for sharper mental math and better decision-making.

FAQs—Frequently Asking Questions

Can subtraction be performed on more than two numbers?

Yes, you can solve a subtraction problem with more than two numbers. For example, 20 − 5 − 3 = 12. However, unlike addition, it is not associative, so the order matters.

Why is subtraction not commutative?

Subtraction is not commutative because changing the order of numbers changes the result. For example, 10 − 3 ≠ 3 − 10.

What is the difference between subtraction and taking the absolute difference?

Subtraction gives the signed difference (which may be negative), while the absolute difference gives the positive distance between two numbers, regardless of order.

How is subtraction related to addition?

Subtraction is the inverse operation of addition. If a − b = c, then c + b = a. Understanding this helps in solving equations and checking answers.

What happens when you subtract a number from itself?

When you subtract a number from itself, the result is always zero. For example, 7 − 7 = 0.