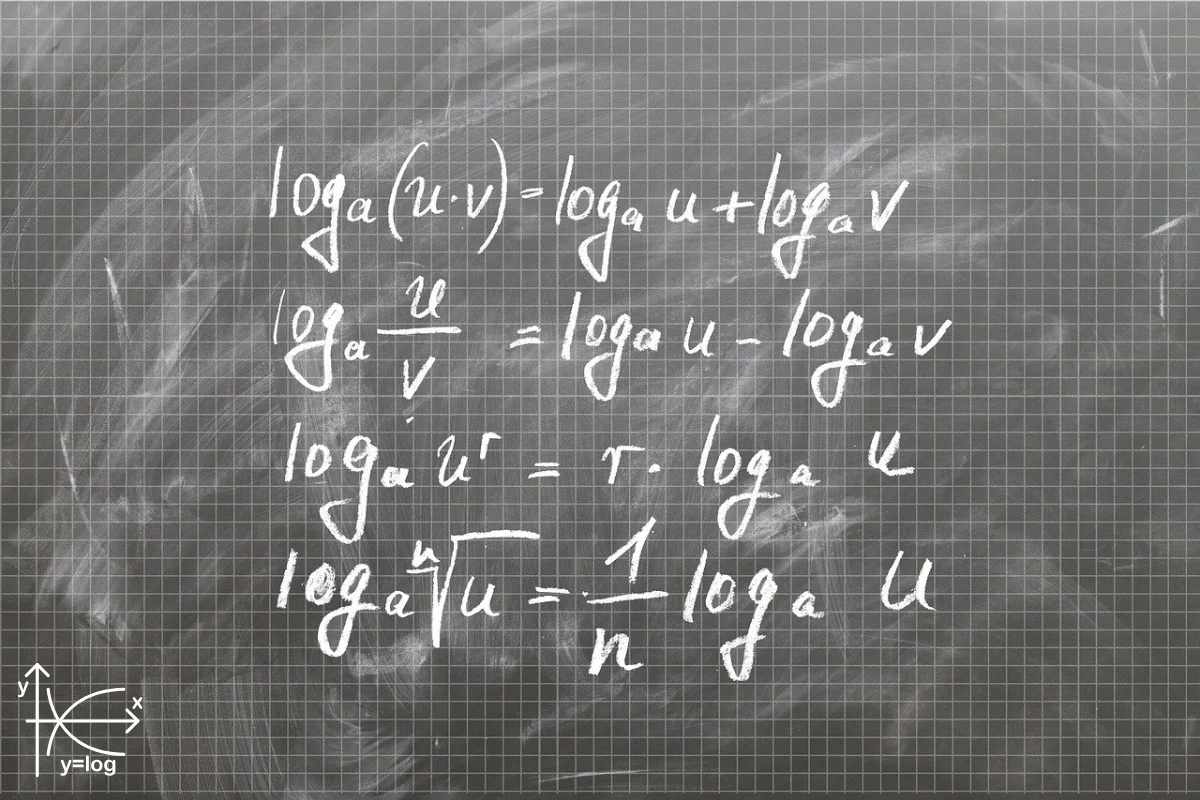Rules of Logarithms
By Alex David
Logarithms can be tricky at first—especially when you are faced with complex expressions or large numbers. Their unfamiliar notation and strange behavior may confuse students and early beginners. But that is where the rules of logarithms come in handy. These rules simplify logarithmic expressions and make calculations simple.
How to Solve Logarithmic Expressions?
Solving logarithmic expressions involves the use of properties of logarithms or rules of logarithms to simplify them. These rules are the fundamental base in algebra and are derived from the definition of logarithms.
Rules of logarithms generally refer to the foundational properties that describe how logarithms work, such as the identity and inverse rules. In contrast, the laws of logarithms are specific formulas, like the product, quotient, and power laws, applied to manipulate and solve logarithmic expressions. However, in the syllabi of many schools and textbooks, these two categories are often combined and presented as a single list of logarithmic formulas. As a result, students may not realize the conceptual distinction between foundational rules and operational laws, even though both serve equally crucial roles in simplifying logarithmic computations.
What are Rules of Logarithms ?
Rules of logarithms are the set of rules that are useful in the simplification and manipulation of logarithmic function expressions. These rules create relationships between exponential and logarithmic forms. It is helpful in solving complex logarithmic computations.
What are the Laws of Logarithms?
The laws of logarithms are the fundamental rules that govern how logarithms behave mathematically. These laws are helpful in simplifying logarithmic expressions.
Difference Between Rules of Logarithms and Laws of Logarithm
This is something that often confuses students. Usually early students mix up these two different terms— but here is a clear and simple concept:
| Aspect | Rules of Logarithms | Laws of Logarithm |
| Definition | These rules are general principles about how logarithms work. | Laws of logarithms are specific formulas or identities that are used to simplify and manipulate logarithmic expressions. |
| Purpose | These are used to understand how logs behave in different mathematical contexts. | These are used to perform different operations like addition, subtraction, exponentiation on logs. |
| Example | ||
| Context of Use | These are basic properties that are helpful when you are learning about logs. | These are tools for solving logarithmic expressions and equations. |
| Relation | These are the foundations or basics of logarithms. | These are applications or extensions of those basic rules. |
Concept
In simple terms, the rules of logarithms refer to what a logarithm actually is, and the laws of logarithms refer to how logarithms behave in operations.
Rules of Logarithms
Logarithmic expressions often look complex at first glance, but these expressions follow a set of structured principles known as the laws and rules of logarithms. These mathematical tools simplify the process of working with logarithms by defining how they behave in various operations like multiplication, division, exponentiation, and base conversion.
The importance of these laws and rules of logarithms lies in their ability to transform complicated logarithmic expressions into simpler forms, making them essential in algebra, calculus, computer science, and fields involving exponential data. Although the terms laws and rules of logarithms are sometimes used interchangeably, there is a subtle difference between them.

Product Rule
“The product rule of logarithms is used to express the logarithm of a product as the sum of logs.”
Concept
This is the first and basic rule among rules of logarithms. It explains the relationship between exponents and logarithms. As you know, logarithms are the inverse of exponents, and when you multiply numbers with the same base in exponents, you add the exponents; the same logic applies to logarithms — but in reverse.
Mathematical Form
![]()
where,
- b is the base of logarithms
- x and y are the positive real numbers.
Example
![]()
Application
- Computer Science: Simplifying complex logarithmic expressions when analyzing algorithms (like Big O notation for time complexity).
- Physics: Rules of logarithms play an important role in signal processing and sound intensity calculations where multiple factors are multiplied together.
- Finance: In compound interest problems where multiple rates or factors are combined.
- Algebraic Simplification: Helps break down complex logarithmic problems into smaller, manageable parts.
Quotient Rule
“The quotient rule of logarithms is used to express the logarithm of a quotient as the difference of logs.”
Concept
This rule comes from the property of exponents where dividing numbers with the same base means subtracting their exponents.
Mathematical Form
![]()
Example
![]()
![]()
Application
- Computer Science: Useful for simplifying time complexity expressions involving division in algorithms
- Physics & Engineering: Helps simplify ratios in signal processing, decibel calculations, and other logarithmic measurements
- Finance: In logarithmic models involving ratios or comparisons of growth rates
- Algebra & Calculus: Essential for breaking down complex logarithmic equations and expressions into simpler parts for easier solving
Power Rule
“The logarithm of a number raised to a power is equal to the exponent multiplied by the logarithm of the base number.”
Concept
This rule is based on the property of exponents that multiplying exponents means adding their powers. Since logarithms deal with exponents, raising a number to a power inside a log means multiplying that power by the log of the base number.
Mathematical Form
![]()
Example
![]()
![]()
Application
- Computer Science: Simplifying logarithmic time or space complexity expressions involving powers.
- Physics: In exponential decay or growth models where values are raised to a power.
- Finance: In compound interest and growth models where powers of factors appear inside logarithmic formulas.
- Calculus: Helpful in logarithmic differentiation when dealing with functions raised to a power.
- Algebraic Simplification: Makes it easier to handle large exponents inside logarithmic expressions by converting multiplication into addition.

Reciprocal Rule
“The log of a reciprocal rule states that the logarithm of the reciprocal of a number is equal to the negative of the logarithm of the number itself.”
Concept
This rule is the same as the exponent property that the reciprocal of a number is the same as raising it to the power of −1.
Mathematical Form
![]()
Example
![]()
Application
- Finance: When working with inverse growth rates or depreciation calculations.
- Computer Science: Inverting logarithmic time complexities in certain algorithm analyses.
Physics: Inverting ratios or decay factors in signal processing. - Algebra & Calculus: Simplifying expressions involving reciprocals inside logarithms.
Root Rule
“The log of a root rule states that the logarithm of the nth root of a number is equal to the logarithm of the number divided by n. It turns the root operation inside a logarithm into division outside the log.”
Concept
This rules of logarithms comes from converting a root into a fractional exponent.
Mathematical Form
![]()
Example
![]()
Application
- Physics: Simplifying square root or cube root values in logarithmic form for calculations involving resistance, sound intensity, or pressure.
- Finance: Working with annualized returns or depreciation rates over a certain number of years.
- Computer Science: When breaking down logarithmic expressions involving fractional exponents or root operations.
- Algebra & Calculus: Simplifying complex expressions or equations that include roots inside logarithms.

Identity Rule
“The logarithm of a number b with base b is always 1.”
Mathematical Form
![]()
Concept
The Identity Rule of Logarithms is based on the fundamental definition of a logarithm. It states that the logarithm of a number to its own base is always equal to 1.
Whenever the number inside the logarithm is the same as its base, the result will always be 1, no matter what the base is (as long as it’s positive and not equal to 1).
Example
![]()
Applications
The identity rule is used
- In logarithmic equations, it is used to cancel out log terms.
- In computer science, especially when working with algorithms and base-2 logs.
- In mathematical proofs and simplifying complex expressions.
- In scientific calculators to recognize when results simplify to 1.
Zero Rule
“The logarithm of 1 to any positive base b (≠1) is always 0.”
Concept
As you know in the topic of exponents, b0 = 1. now you may think about what the relationship is between this and the above-zero rule. The question log-(1) = ? means, “To what power must b be raised to get 1?” Answer: 0.
Mathematical Form
![]()
Example
![]()
Inverse Rule
“If the base of the logarithm and the base of the exponent are the same, they cancel out — leaving just the exponent.”
Concept
The Inverse Rule of Logarithms is based on the idea that logarithms and exponents are inverse operations. It states that if a logarithm has the same base as the base of the exponent inside it, the log and the exponent cancel each other out — leaving only the exponent.
Mathematical Form
![]()
Example
![]()

Change of Base Rule
“A logarithm with any base b can be converted to a different base k (commonly 10 or e) by dividing two logarithms — both with the new base k.”
Concept
Most of the calculators only support log base 10 and log base. For calculating, log2(16)we use a change of base rule to rewrite it by using log base 10 or log base e.
Mathematical Form
![]()
Example
![]()
Application
- Computer Science: Binary logs often require conversion for calculator use.
- Engineering & Physics: Base conversion in signal processing or decibel calculations.
- Finance: Converting logs in compound interest problems.
- Calculus: Simplifying expressions during differentiation or integration.
Conclusion
| Name | Mathematical Form | Example |
| Product Rule | ||
| Quotient Rule | ||
| Power Rule | ||
| Reciprocal Rule | ||
| Root Rule | ||
| Identity Rule | ||
| Zero Rule | ||
| Inverse Rule | ||
| Change of Base Rule |
Frequently Asking Questions (FAQs)
Q # 01: What are the main rules of logarithms?
The main rules and laws of logarithms include the Identity Rule, Zero Rule, Inverse Rule, Product Rule, Quotient Rule, Power Rule, Log of a Reciprocal, Log of a Root, and Change of Base Rule. These help simplify and manipulate logarithmic expressions efficiently.
Q # 02: Why are rules of logarithms important?
Rules of logarithms are important because they allow us to break down, simplify, and solve complex logarithmic expressions and equations. They also form the foundation for solving real-world problems in areas like computer science, physics, finance, and engineering.
Q # 03: What is the difference between rules of logarithms and laws of logarithms?
Rules of logarithms refer to the basic properties that describe how logarithms work, such as the identity and zero rules. Laws of logarithms, on the other hand, are specific formulas like the product, quotient, and power laws, used to simplify and manipulate logarithmic expressions. In many school syllabi, these two terms are often combined and taught together.
Q # 04: How many laws of logarithms are there?
Typically, there are three core laws of logarithms:
- Product Law
- Quotient Law
- Power Law
However, additional rules like the identity, zero, inverse, change of base, log of reciprocal, and log of a root are also widely taught for more comprehensive problem-solving.
Q # 05: Can the base of a logarithm be any number?
The base of a logarithm can be any positive real number except 1. Common bases used are 10 (common logarithm), e (natural logarithm), and 2 (binary logarithm).
Q # 06: What is the product rule of Logarithms used for?
The product rule simplifies the logarithm of a product into the sum of individual logarithms. It’s useful for breaking down large multiplication problems or simplifying logarithmic expressions in algebra and calculus.
Q # 07: How does the Quotient Rule of Logarithms work?
The Quotient Rule states that the log of a quotient is equal to the difference between the logs of the numerator and denominator. It makes it easier to handle division operations within logarithmic expressions.
Q # 08: What is the power rule in logarithms?
The power rule allows you to move the exponent of a number inside a logarithm to the front as a multiplier. This simplifies complex exponential expressions inside a log.
Q # 09: How is the change of base rule used in logarithms?
The change of base rule lets you convert a logarithm from one base to another, usually to base 10 or e, making it compatible with standard calculators.
Q # 10: Are there any common mistakes when using rules of logarithms ?
Yes. Common mistakes include
- Forgetting domain restrictions (logs of zero or negative numbers are undefined)
- Incorrectly applying the Product or Quotient Rule
- Mixing up the base in the Change of Base Rule
- Missing negative signs when dealing with reciprocals
Q # 11: Can you take the logarithm of a negative number?
No. The logarithm of a negative number is undefined in the real number system because there’s no real exponent that can make a positive base produce a negative result.
Q # 12: What are some real-life applications of rules of logarithms ?
Rules of logarithms are applied in many areas, including
- Computer Science: Time complexity analysis
- Physics: Measuring sound intensity (decibels) and earthquake magnitude (Richter scale)
- Finance: Calculating compound interest and investment growth
- Engineering: Signal processing and electrical circuits