Division

By Alex David

April 4, 2025

Ever wondered how to split things equally? Whether it’s sharing chocolates, dividing expenses, or solving math problems, division is the key! Learn the fastest mental math tricks and long division strategies to make calculations easier!

Mental math helps you in this regard. For this problem, just remember a few rules through which you can easily divide the chocolates equally among your friends! The way through which you distribute chocolates among your friends is one of the fundamental operators of mathematics known as division.

What is Division?

It is one of the basic arithmetic operators. It is defined as:

“Division is a mathematical process of splitting a quantity into equal parts or determining how many times one value fits into another.”

It tells us how many times one number (the divisor) fits into another number (the dividend).

Basic Concept:

The basic concept is as; it is the knowledge of sharing, splitting, and understanding the relationship between a complete number and its parts. It is the understanding of how a quantity can be broken into smaller, equal portions. At its deepest concept, division reveals the relationships of numbers, showing how one quantity can relate to another in a multiplicative or fractional manner.

Symbols:

A symbol is a name of sense that enables one to recognize the operation and give the answers to multiple questions, like how to perform this operation. In this case, there are different symbols that are applicable according to the scenario.

÷

The first one is very simple and mostly used in mathematics.

Example:

12 ÷ 3 = 4

/ (forward slash)

It is the second symbol but frequently used in programming and calculators.

Example:

12/3 =4

Colon (:)

This symbol is mostly used for ratio or proportion.

Example:

12:3 = 4

Square Root

This is the basic and frequently used symbol. It is mostly used for long division.

Position in PEMDAS:

PEMDAS is the name of understanding the order of operations in mathematics, ensuring calculations are done correctly and consistently. PEMDAS stands for:

P: Parentheses (solve expressions inside parentheses first)

E: Exponents (evaluate powers and roots next)

MD: Multiplication and Division (work from left to right)

AS: Addition and Subtraction (work from left to right)

It is at number three. If multiplication and division appear simultaneously in the question, then the left-to-right rule is applicable.

Different Parts:

It consists of the following four main parts:

Dividend:

Definition: The number being divided in this operation is called the dividend.
Concept: This is the total amount that you are trying to split into equal parts.
Example: In this equation 25 ÷ 5 = 5, the dividend is 25. This is the number you are dividing into smaller parts.

Divisor:

Definition: The number by which the dividend is being divided is called the divisor.
Concept: This is the number that indicates how many equal parts you are splitting the dividend into. Essentially, it’s the name of “group size” or “equal portions” you’re dividing into.
Example: In 25 ÷ 5 = 5, the divisor is 5. You are dividing the dividend (25) into groups of 5.

Quotient:

Definition: Basically, it is the number of equal parts you get when you divide the dividend by the divisor.
Concept: This tells you how many times the divisor can “fit” into the dividend.
Example: In 25 ÷ 5 = 5, the quotient is 5. This means that when you divide 25 by 5, you get 5 equal parts.

Remainder:

Definition: The remainder is what’s left over when the dividend cannot be divided evenly by the divisor.
Explanation: This happens when the results in a partial or incomplete part (i.e., not a whole number). The remainder is the leftover part after the division.
Example: In 13 ÷ 5 = 2 with a remainder of 3, the remainder is 3. This means that when 13 is divided by 5, 2 full groups of 5 can be formed, but there are 3 left over.

Formulas:

Sometimes for the better understanding, we use the basic formulas. These formulas serve as a foundation for understanding how numbers interact, making problem-solving entertaining and efficient. By using these formulas, you will learn about different properties of division. This approach fosters a deeper understanding, enabling individuals to tackle problems confidently

Basic Formula:

Dividend ÷ Divisor = Quotient

Example:

12 ÷ 3 = 4

Remainder Formula:

Dividend = (Divisor × Quotient) + Remainder

Example:

13 ÷ 5 = 2 remainder 3

So, 13 = (5 × 2) + 3

For Checking Answer:

Quotient × Divisor + Remainder = Dividend

Example:

If 13 ÷ 5 = 2 remainder 3

then: (2 × 5) + 3 = 13

Relationship Between Multiplication & Division:

Division and multiplication are opposite to each other.

Dividend = Divisor × Quotient

Example:

If 12 ÷ 3 = 4

then: 12 = 3 × 4

Fraction Representation:

Dividend ÷ Divisor = Dividend Divisor

Example:

12 ÷ 3 = 123

Average Formula:

Average = Sum of Terms/Number of Terms

Example:

The average of 10, 20, and 30 is as follows:

(10 + 20 + 30) / 3 = 60 / 3 = 20

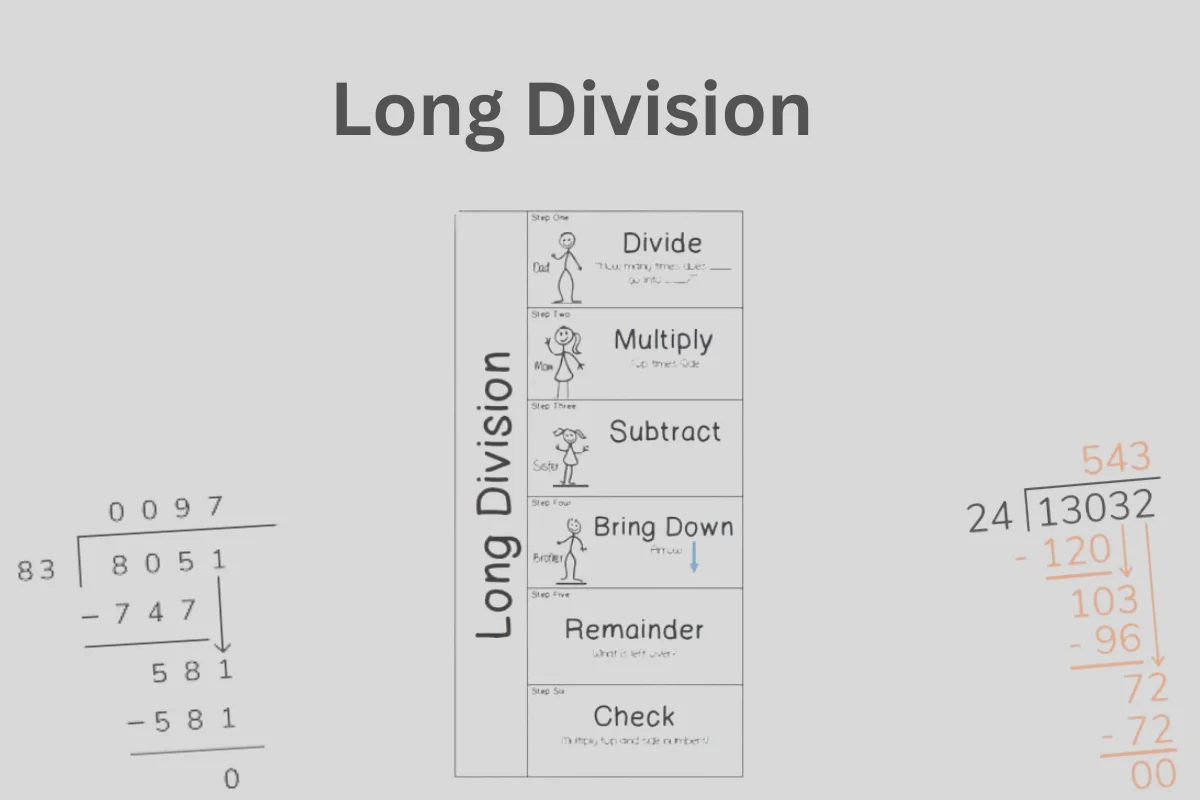
Long Division:

Long division is a mathematical method for dividing large numbers. It is a step-by-step procedure to break down the large and complex into smaller and manageable parts.

It is often used when you can’t easily divide the numbers in your head. Long division breaks the long division problem into manageable steps, making it easier to calculate.

Mental Math Concept for Long Division:

Mental math simplifies the long division into an easy, tricky way. That tricky way is DMSBR steps (Divide, Multiply, Subtract, Bring Down, Repeat) of long division by allowing quicker estimations and calculations. Simply follow these five repeated steps to make long division your power.

Conclusion:

Division is a fundamental mathematical operation that simplifies complex problems by breaking equations into manageable parts. It has a crucial role in everyday problem-solving. Understanding its parts—dividend, divisor, quotient, remainder—helps to understand its logic and build a solid foundation for arithmetic and problem-solving skills.

For this, different basic formulas, such as the basic formula, remainders formula, and the relationship with multiplication, enhance understanding. It is the ability to develop your logical reasoning, critical thinking, and problem-solving abilities.